Center for Artificial Low Dimensional Electronic Systems

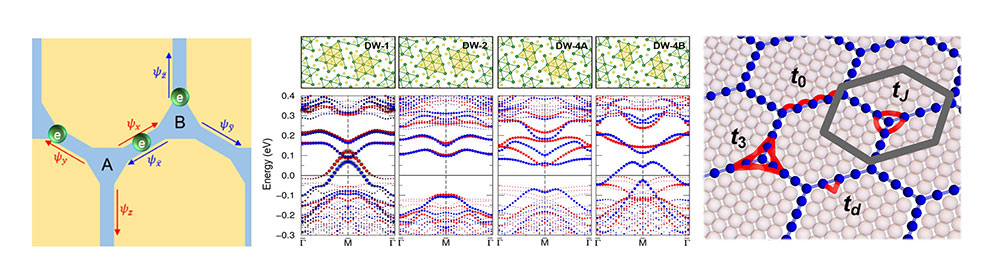
Recently, we are witnessing a proliferating set of materials exhibiting 2D conducting networks of 1D metals along with possibly the inter-dimensional physics crossing over from one to two dimensions. Several charge-density wave materials such as1T-TaS₂, 1T-TiSe₂, Helium atoms absorbed on graphite, and moiré systems such as twisted bilayer graphene are the prominent examples. These materials realize remarkably broad sets of emergent quantum phenomena such as spin liquid, metal-insulator transition, Anderson localization, topological band structures, and superconductivity. The origin of these phenomena has not been satisfactorily clarified, due in most part to the lack of theoretical tools available for unraveling the nature of network electrons.

Our group developed a theoretical framework for the low-energy physics of the network systems. Combining tight-binding models, density-functional theory, and phenomenological scattering models, we have demonstrated that the network superstructures host a number of intriguing electronic states such as non-Fermi liquids, a cascade of anomalously stable flat bands, and higher-order topological insulators. In particular, for 1T-TaS₂ we succeeded in identifying various in-gap states in discommensurate domain walls by density functional theory calculations. By combining with the field theoretic investigation, we also discovered that the network superstructure is very susceptible to develop a superconductivity, which can potentially explain the “universal” superconductivity in these network materials.

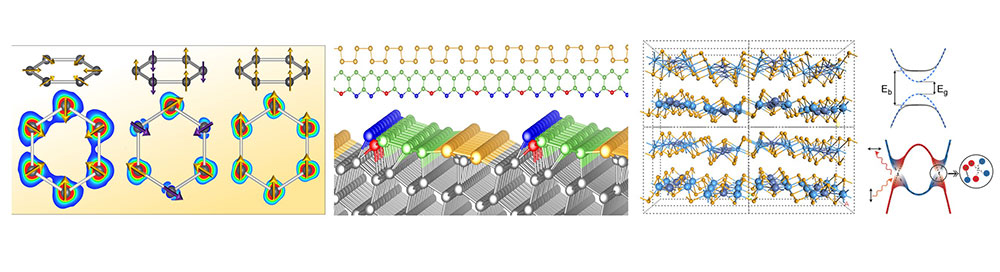
One of the most important roles that the theory team plays is the simulation of electronic and structural properties of various materials, which are experimentally investigated by the other groups in the center. The density functional theory (DFT) is a computational approach, which can be applied to a broad range of quantum materials. Using this versatile tool, we uncovered electronic structures of a number of novel materials. For example, we found the formation of unusual relativistic molecular orbitals within the Pb clusters on IrTe₂ substrate. In another work, we revealed the topological properties of the solitons and their fractional charges in the silicon atomic chains formed along the step edge of Si(553)-Au surface. Furthermore, the DFT simulation also helps to identify the elusive quantum states such as exciton condensate in Ta₂NiSe₅, where we have systematically investigated the excitonic properties and correlation effects. The computational approach complements the center’s experimental search of the new types of low dimensional electronic systems, which may lead to a new paradigm in device technology.

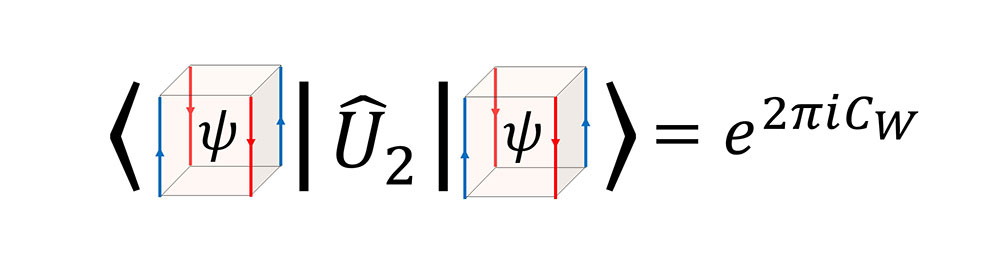
The topological phase is the central theme of modern condensed matter physics. The most well-known examples are topological band insulators and quantum Hall states. More recently, the higher-order topological insulators have been discovered and received huge attentions both from experiment and theory. Unlike their ancestors, their non-trivial topology manifests only at the corners and hinges. Despite rapid developments, there are still many important research problems about these insulators. For example, the absolute number of materials realizing the higher-order topology is very small and hence it is desirable to search more material candidates for the topology. Furthermore, it is entirely an open problem how the higher-order topology can be defined beyond the band insulators and detected in strongly correlated systems. Motivated from these, we have constructed a numerically-efficient scheme for defining and detecting the higher-order topology from many-body ground state wavefunctions. At the same time, we also demonstrated that the higher-order topology is generically expected in twisted bilayer graphene.

Another class of topological phases is the states with fractional excitations. These excitations, also known as “anyons”, have fractional statistics, which is neither bosonic nor fermionic, and can be utilized in decoherence-free quantum computers. Recently, we have developed novel theoretical protocols for classifying 2D states with anyons. Our approach reproduced many known results but also discovered several new states. We are currently looking for the condensed matter realizations of these newly-discovered states.